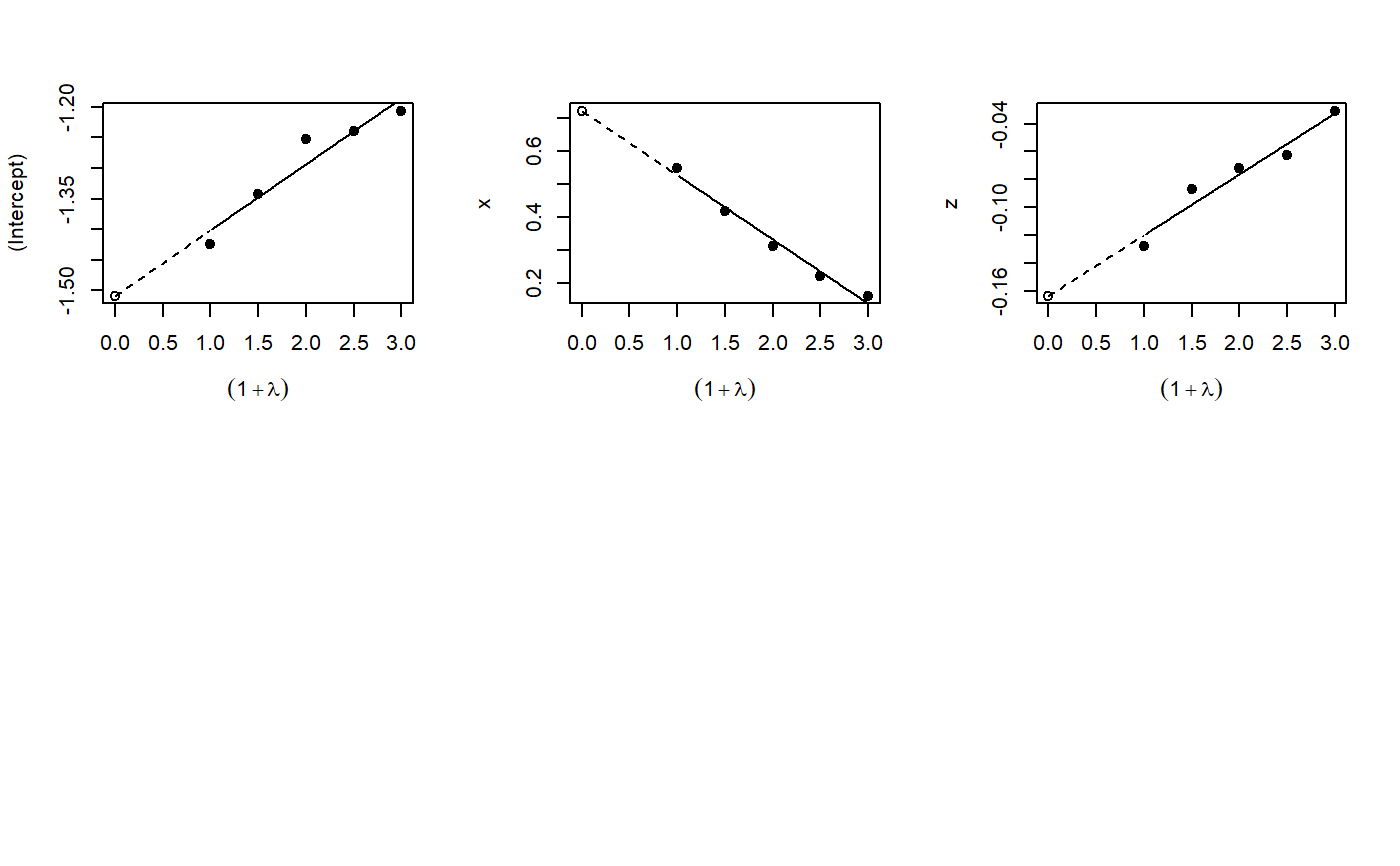Misclassification in models using MCSIMEX

Source: R/mcsimex.R

Implementation of the misclassification MCSIMEX algorithm as described by Küchenhoff, Mwalili and Lesaffre.

mcsimex(model, SIMEXvariable, mc.matrix, lambda = c(0.5, 1, 1.5, 2),
  B = 100, fitting.method = "quadratic",
  jackknife.estimation = "quadratic", asymptotic = TRUE)

# S3 method for mcsimex
plot(x, xlab = expression((1 + lambda)),
  ylab = colnames(b[, -1]), ask = FALSE, show = rep(TRUE, NCOL(b) -
  1), ...)

# S3 method for mcsimex
predict(object, newdata, ...)

# S3 method for mcsimex
print(x, digits = max(3, getOption("digits") - 3), ...)

# S3 method for summary.mcsimex
print(x, digits = max(3, getOption("digits") -
  3), ...)

# S3 method for mcsimex
summary(object, ...)

# S3 method for mcsimex
refit(object, fitting.method = "quadratic",
  jackknife.estimation = "quadratic", asymptotic = TRUE, ...)

Arguments

model

the naive model, the misclassified variable must be a factor
SIMEXvariable

vector of names of the variables for which the MCSIMEX-method should be applied
mc.matrix

if one variable is misclassified it can be a matrix. If more than one variable is misclassified it must be a list of the misclassification matrices, names must match with the SIMEXvariable names, column- and row-names must match with the factor levels. If a special misclassification is desired, the name of a function can be specified (see details)
lambda

vector of exponents for the misclassification matrix (without 0)
B

number of iterations for each lambda
fitting.method

linear, quadratic and loglinear are implemented (first 4 letters are enough)
jackknife.estimation

specifying the extrapolation method for jackknife variance estimation. Can be set to FALSE if it should not be performed
asymptotic

logical, indicating if asymptotic variance estimation should be done, the option x = TRUE must be enabled in the naive model
x

object of class 'mcsimex'
xlab

optional name for the X-Axis
ylab

vector containing the names for the Y-Axis
ask

ogical. If TRUE, the user is asked for input, before a new figure is drawn
show

vector of logicals indicating for which variables a plot should be produced
…

arguments passed to other functions
object

object of class 'mcsimex'
newdata

optionally, a data frame in which to look for variables with which to predict. If omitted, the fitted linear predictors are used
digits

number of digits to be printed

Value

An object of class 'mcsimex' which contains:

coefficients

corrected coefficients of the MCSIMEX model,

SIMEX.estimates

the MCSIMEX-estimates of the coefficients for each lambda,

lambda

the values of lambda,

model

the naive model,

mc.matrix

the misclassification matrix,

B

the number of iterations,

extrapolation

the model object of the extrapolation step,

fitting.method

the fitting method used in the extrapolation step,

SIMEXvariable

name of the SIMEXvariables,

call

the function call,

variance.jackknife

the jackknife variance estimates,

extrapolation.variance

the model object of the variance extrapolation,

variance.jackknife.lambda

the data set for the extrapolation,

variance.asymptotic

the asymptotic variance estimates,

theta

all estimated coefficients for each lambda and B,

...

Details

If mc.matrix is a function the first argument of that function must be the whole dataset used in the naive model, the second argument must be the exponent (lambda) for the misclassification. The function must return a data.frame containing the misclassified SIMEXvariable. An example can be found below.

Asymptotic variance estimation is only implemented for lm and glm

The loglinear fit has the form g(lambda, GAMMA) = exp(gamma0 + gamma1 * lambda). It is realized via the log() function. To avoid negative values the minimum +1 of the dataset is added and after the prediction later substracted exp(predict(...)) - min(data) - 1.

The 'log2' fit is fitted via the nls() function for direct fitting of the model y ~ exp(gamma.0 + gamma.1 * lambda). As starting values the results of a LS-fit to a linear model with a log transformed response are used. If nls does not converge, the model with the starting values is returned.

refit() refits the object with a different extrapolation function.

Methods (by generic)

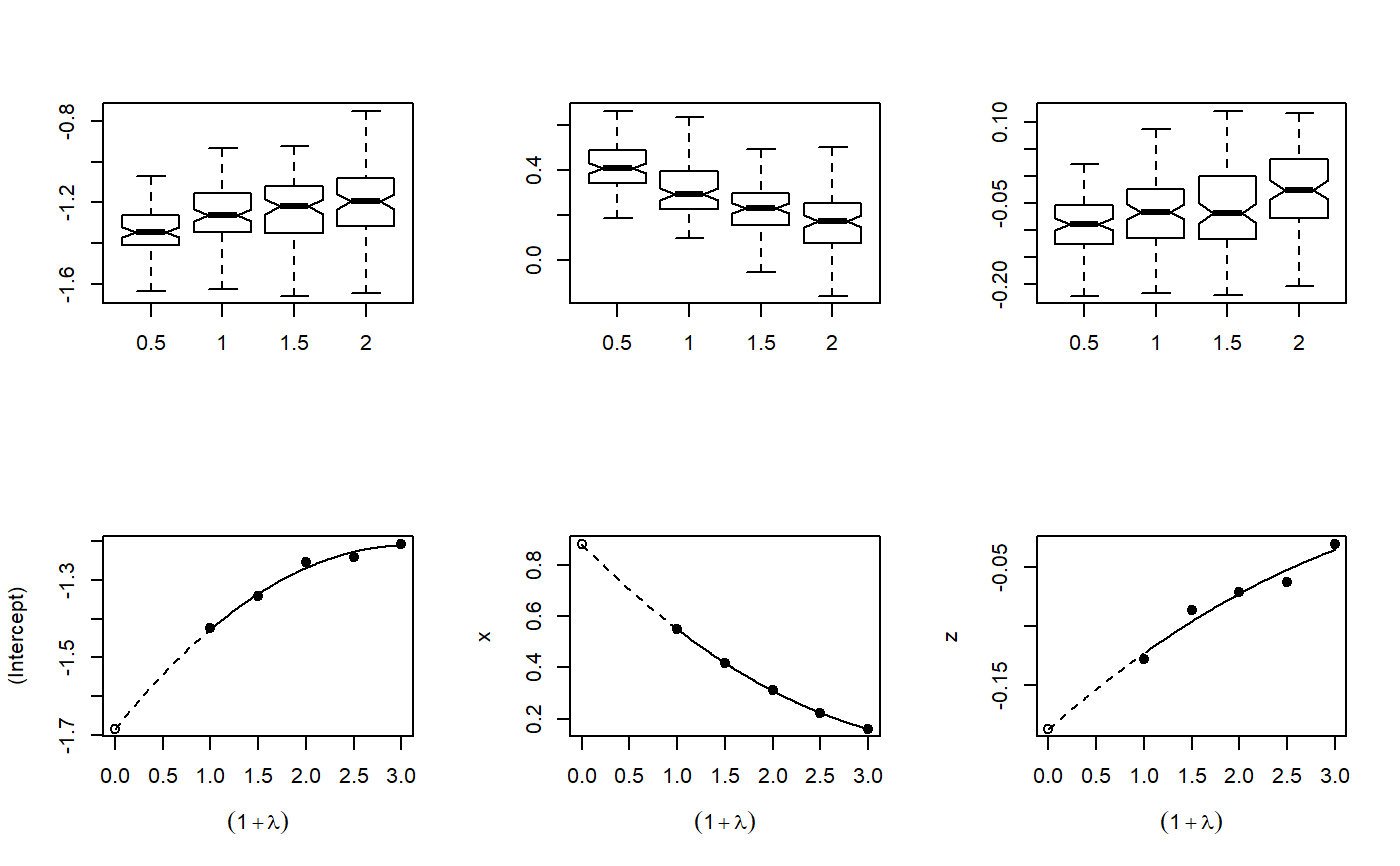
  • plot: Plots of the simulation and extrapolation

  • predict: Predict with mcsimex correction

  • print: Nice printing

  • print: Print summary nicely

  • summary: Summary for mcsimex

  • refit: Refits the model with a different extrapolation function

References

Küchenhoff, H., Mwalili, S. M. and Lesaffre, E. (2006) A general method for dealing with misclassification in regression: The Misclassification SIMEX. Biometrics, 62, 85 -- 96

Küchenhoff, H., Lederer, W. and E. Lesaffre. (2006) Asymptotic Variance Estimation for the Misclassification SIMEX. Computational Statistics and Data Analysis, 51, 6197 -- 6211

Lederer, W. and Küchenhoff, H. (2006) A short introduction to the SIMEX and MCSIMEX. R News, 6(4), 26--31

See also

misclass, simex

Examples

x <- rnorm(200, 0, 1.142)
z <- rnorm(200, 0, 2)
y <- factor(rbinom(200, 1, (1 / (1 + exp(-1 * (-2 + 1.5 * x -0.5 * z))))))
Pi <- matrix(data = c(0.9, 0.1, 0.3, 0.7), nrow = 2, byrow = FALSE)
dimnames(Pi) <- list(levels(y), levels(y))
ystar <- misclass(data.frame(y), list(y = Pi), k = 1)[, 1]
naive.model <- glm(ystar ~ x + z, family = binomial, x = TRUE, y = TRUE)
true.model  <- glm(y ~ x + z, family = binomial)
simex.model <- mcsimex(naive.model, mc.matrix = Pi, SIMEXvariable = "ystar")

op <- par(mfrow = c(2, 3))
invisible(lapply(simex.model$theta, boxplot, notch = TRUE, outline = FALSE,
                 names = c(0.5, 1, 1.5, 2)))
                 plot(simex.model)
simex.model2 <- refit(simex.model, "line")
plot(simex.model2)
par(op)

# example using polr from the MASS package
# NOT RUN {
if(require(MASS)) {
  yord <- cut((1 / (1 + exp(-1 * (-2 + 1.5 * x -0.5 * z)))), 3, ordered=TRUE)
  Pi3 <- matrix(data = c(0.8, 0.1, 0.1, 0.2, 0.7, 0.1, 0.1, 0.2, 0.7), nrow = 3, byrow = FALSE)
  dimnames(Pi3) <- list(levels(yord), levels(yord))
  ystarord <- misclass(data.frame(yord), list(yord = Pi3), k = 1)[, 1]
  naive.ord.model <- polr(ystarord ~ x + z, Hess = TRUE)
  simex.ord.model <- mcsimex(naive.ord.model, mc.matrix = Pi3,
      SIMEXvariable = "ystarord", asymptotic=FALSE)
}
# }

# example for a function which can be supplied to the function mcsimex()
# "ystar" is the variable which is to be misclassified
# using the example above

# NOT RUN {
my.misclass <- function (datas, k) {
    ystar <- datas$"ystar"
    p1 <- matrix(data = c(0.75, 0.25, 0.25, 0.75), nrow = 2, byrow = FALSE)
    colnames(p1) <- levels(ystar)
    rownames(p1) <- levels(ystar)
    p0 <- matrix(data = c(0.8, 0.2, 0.2, 0.8), nrow = 2, byrow = FALSE)

    colnames(p0) <- levels(ystar)
    rownames(p0) <- levels(ystar)
    ystar[datas$x < 0] <-
    misclass(data.frame(ystar = ystar[datas$x < 0]), list(ystar = p1), k = k)[, 1]
    ystar[datas$x > 0] <-
    misclass(data.frame(ystar = ystar[datas$x > 0]), list(ystar = p0), k = k)[, 1]
    ystar <- factor(ystar)
    return(data.frame(ystar))}

simex.model.differential <- mcsimex(naive.model, mc.matrix = "my.misclass", SIMEXvariable = "ystar")
# }